Ostří sekáčů pro elektropneumatická kladiva
Špička sekáče nemusí být ostrá v pravém slova smyslu. Pod slovem „ostrý“ si často představujeme takové ostří, kterým se můžeme pořezat. Možná tato představa vychází z toho, že nejčastějším předmětem, který si v souvislosti s tímto slovem představujeme, je nůž.
Sekáč je v podstatě klín, tak jako nůž. A klín je těleso trojúhelníkového průřezu, přičemž nejčastěji jde o rovnoramenný trojúhelník, kde dvě přilehlé odvěsny svírají úhel klínu (obr. 1), který je však u těchto dvou předmětů zcela odlišný.
Proto za ostré považujeme takové sekáče, které mají správné úhly ostří. A tyto úhly souvisí zejména s podkladovým materiálem, který hodláme obrábět.
Možná nám to připadá v dnešní době automatizace a robotizace divné (přiznám se, že i mně), ale klín je stroj. Přesněji – patří do kategorie jednoduchých strojů spolu s několika blízkými kolegy, například s pákou nebo kolem na hřídeli.

Obr. 1. Klín v řezu – rovnoramenný trojúhelník se dvěma odvěsnami a,b svírajícími úhel α

Obr. 2. Přitažlivý muž  s ostrým pazourkem
s ostrým pazourkem
Pěstní klín je známý nástroj již z období staršího paleolitu. Nevěřili byste, ale podle jedné z Darwinových teorií jsou pěstní klíny nejstarší umělecká díla a jejich výroba byla jedním ze způsobů komunikace. Muži je totiž vyráběli (obr. 2) i proto, aby se předváděli před ženami. Ženy si zase všímaly zejména jejich jemné motoriky, svědomitosti, vytrvalosti a také jejich vztahu k materiálům – tedy k surovinám, které byly pro ně v té době pro výrobu pěstního klínu potřebné a velmi cenné.
Klín má hodně společného s nakloněnou rovinou a s tou má zase hodně společného například šroub. Vždyť šroub je vlastně svinutá nakloněná rovina a stoupání jeho závitů není nic jiného než „náklon“, tedy úhel nakloněné roviny. Alespoň vidíme, jak mnohé technické věci mezi sebou souvisí. Vždyť kdo by si v každodenním životě pomyslel, že sekáč a šroub mají něco společného?
Naši předkové jistě nevěděli, jakou sílu dokáží vyvinout jedním jediným úderem do klínu (obr. 3).
Přesné výpočty takového úderu jsou samozřejmě možné, ale i když se jedná o jednoduché stroje, výpočty až tak jednoduché nejsou. Museli bychom oprášit znalosti z goniometrických funkcí, protože tangens, sinus a kosinus jsou k tomu nezbytně nutné. Zkusíme se proto obejít bez nich, i když trochu matematiky zde bude.
Každý, kdo štípal dřevo a navíc, když byl nucen používat i klíny ví, jaká to je namáhavá práce.
Ale věděli jste, že středně silný muž se 7kg těžkým zednickým kladivem a vhodným klínem může vyvinout jednou jedinou dobře vedenou ranou sílu 10.000 až 15.000 kilopondů? Jednoduše řečeno, jde o sílu odpovídající 10 až 15 tunám jedním jediným úderem!

Obr. 3. Úder na klín usnadňuje práci
Současným fyzikům (kdyby četli tento článek) se omlouvám. Ne náhodou jsem uvedl starší jednotku síly. Jeden kilopond (kp) je síla vyvolaná tíží závaží o hmotnosti 1kg v gravitačním poli Země. Je pravdou, že dnes se síla udává v Newtonech (N) a 1kp = 9,80665N. Správně by mělo být, že ten chlap s dobře mířeným úderem vyvolal sílu 98.066 až 147.099 Newtonů. Co myslíte, který z údajů je lepší pro představivost: 10 až 15 tun nebo 98.066 až 147.099 Newtonů? Nebylo to kdysi všechno jaksi jasnější?
Princip klínu

Obr. 4. Princip klínu
Síla F, kterou působí dělník na klín (obr. 4) vyrovnává zatížení podkladového tělesa ve stejném poměru, jako jsou rozměry klínu:

Sílu F umíme z poměrů stran snadno vypočítat i jednoduchou úvahou. Představme si například, že na klín tlačí závaží o hmotnosti Fg = 300kg , délka klínu a=5m a šířka klínu b=1m. Jakou silou musí tlačit dělník klín, aby byl systém v rovnováze?
Jelikož a:b je v poměru 5:1, pak i tlak dělníka je 5krát menší než 300kg = 60kg . Kdyby byl tento klín dlouhý 10m a jeho šířka by zůstala nezměněna, dělníkovi by stačilo tlačit silou 30kg.
Mechanickou výhodou klínu je tedy faktor, kterým znásobujeme sílu působící na tento stroj. Jedná se o poměr vstupní a výstupní síly (obr. 5). Vstupní sílu směřovanou do velké plochy koncentrujeme díky klínu do podstatně menší plochy.
Čím bude klín ostřejší, s tím menší námahou vyvineme tutéž sílu, i když po delší dráze. Nebo jinak – čím bude klín ostřejší, tím větší sílu vyvineme při stejné námaze. Delší a tenčí klín má tedy větší mechanickou výhodu než kratší a širší klín.
Úzkou (ostrou) stěnu klínu nazýváme čelo. U sekáčů používáme pojem ostří. Síla, která působí na podstavu klínu, se rozloží ve směru kolmém na boční stěny. U sekáčů místo podstavy klínu používáme pojem hlava sekáče – to je vlastně úderná plocha.

Obr. 5. Vstupní síla (A) a výstupní síly (B)

Obr. 6. Ostrý klín (A) a tupý klín (B): vektorové rozložení sil
Síla úderu, působící na hlavu sekáče, se přenáší na jeho ostří a to působí silou na obrobek podél nakloněných stran – nakloněných rovin, které způsobí, že se obrobek rozdělí, resp. oddělí.
Tato síla se rozloží ve směru kolmém na boční stěny, přičemž tyto složky jsou větší než vstupní síla – a jak již víme, závisí na úhlu, který svírají boční stěny – čím je tento úhel menší, tím jsou síly větší (obr. 6).
Úkolem ostří sekáčů elektropneumatických kladiv (obr. 7) je narušit podklad, do kterého pak následně vnikne ostřejší část špičky sekáče a ta oddělí část obrobku.
Velikost odděleného obrobku souvisí s parametry kladiva – malým sekáčem a kladivem SDS-plus s energií příklepu 2 Joule oddělujeme menší části obrobku než se sekáčem a sekacím kladivem SDS-max nebo kombinovaným kladivem SDS-max s energií příklepu 10 Joule.
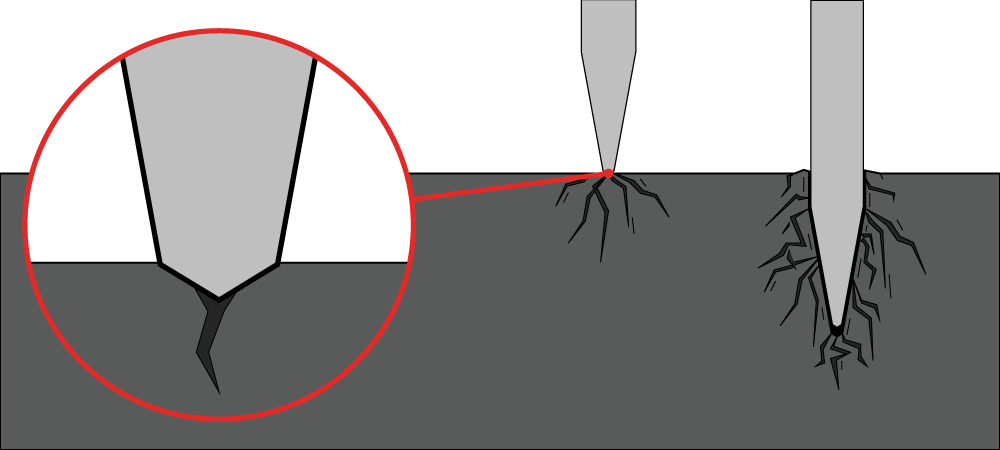
Obr. 7. Ostří sekáče, narušení a následné vniknutí do podkladového materiálu
Pokud se při sekání „zakousneme“ do příliš velkého sousta , sekáč se vzpříčí – rozmačkaný materiál na něj tlačí ze dvou (někdy i z více stran) příliš velkou třecí silou. Tato třecí síla je hlavním „viníkem“ vysokých teplot v oblasti špičky sekáče. Samozřejmě, vysoké teploty od úderů jsou i v oblasti hlavy sekáče.

Obr. 8. Úhly špičatého a plochého sekáče
Stanovený úhel ostří závisí do značné míry na vlastnostech obrobku. Jistě jste si všimli, že sekera má menší úhel než štípací klín. Příliš úzký klín by se totiž vnořil hluboko do materiálu (= velká plocha, velké tření...) a jeho příliš malý úhel by způsobil „zaseknutí“ klínu ve štípaném dřevě, který bychom uvolňovali jen s velkou námahou. Klín se „zaklínil“ – často slyšíme právě takový výstižný výraz pro tento stav.
Ani sekáče do betonu nemají náhodnou geometrii. Krátké, cca 60° ostří přechází do cca 20° úhlu. Tyto hodnoty jsou optimální pro sekání do betonu a je třeba je (alespoň přibližně) dodržovat.
Všimněte si, že špičatý i plochý sekáč (obr. 8) mají v řezu stejný úhel ostří.
Závěr
Podívejte se do kufříku, jestli se tam nenajde sekáč podobný některému z obr. 9.
Je zřejmé, že s takovými sekáči se k dobré produktivitě práce nedopracujeme – bez dobře připraveného sekáče nedosáhneme potřebné efektivity, ať je naše kladivo jakékoli. Takto otupělé sekáče můžeme „oživit“ už jen jejich tepelným zpracováním.
Přitom stačí sekáč krátce, ale průběžně ostřit. K tomu nám v bojových podmínkách stavby stačí mít po ruce malou úhlovou brusku s lamelovým kotoučem zrnitosti 40 nebo 60. Stačí krátce proběhnout po špičce a alespoň trochu se snažit dodržet předepsané úhly.

Obr. 9. Příklady „ostrých“ sekáčů
Klíčová slova: sekáč, klín, elektropneumatická kladiva, ostří sekáčů, kladivo SDS-plus , kladivo SDS-max
Zdroje:
Interní technické a školicí materiály společnosti HERMAN
TED. A Darwinian theory of beauty | Denis Dutton [online]. 2010-11-16, [cit. 2017-05-08]
Bohumil Dobrovolný: Technická fyzika (Praha 1952)

 Česká republika
Česká republika


Petr Šindelář –
Zajímavé
johnny –
zaujimave. zatial som este sekace neostril ale po tomto clanku zacnem.
Toldi Zsuzsanna –
Nagyon tanulságos.
Velmi poučné.
Přeložit text Zobrazit originálPeter Saro –
Dobré. Súhlasím.
Bohuš –
dobre čitanie